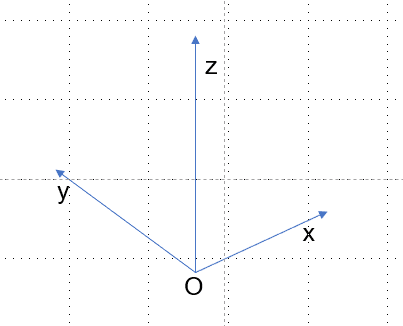绘图基础

首先，需要知道的是matlab三维图的默认坐标轴的位置：面向大家的是 y-z平面，侧面是 x-z 平面，顶底是 x-y 平面。如下图所示

readme

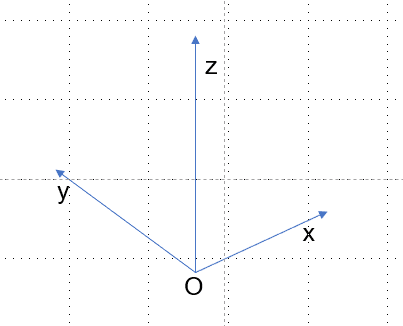
通过该图，我们能进一步了解到其绘图坐标系的原点的位置，如下图所示 coordinate

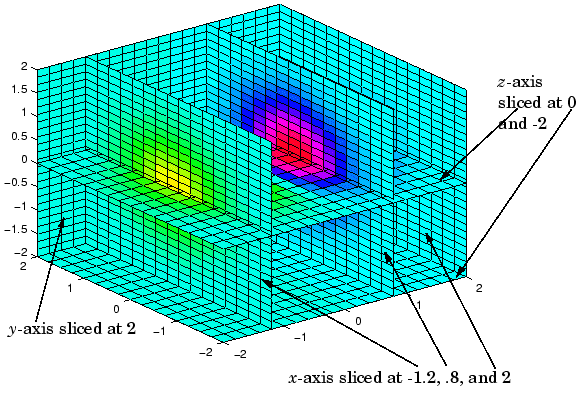
绘制四维图需要采用slice命令，slice命令的两个基本用法如下

1
2
3

% V 是数据体，sx,sy,sz分别为x,y,z方向的切片，X,Y,Z 为坐标值。
slice(V,sx,sy,sz)    % 此命令采用索引绘图，绘图出来的坐标轴的值为索引值
slice(X,Y,Z,V,sx,sy,sz) % 该命令绘制出来的坐标轴的值为真实坐标值。

我们这里选择第二种方式来绘图，以便清楚地解释数据的物理意义。

生成三维坐标网格数据。

由于地震勘探数据的特殊物理意义，Z坐标轴一般为深度或者时间，因此，如果原始数据并非深度或时间，可采用permute函数将数据转换成第三维为深度或时间的数据。

1
2

% 假设原始数据的size为 [nz, nx, ny] = size(T);
T = permute(T, [3 2 1]); % 将第三维和第一维互换

对数据进行上述预处理后，我们开始生成网格数据。生成网格数据的命令为meshgrid。

1
2
3
4

x = linspace(0,1,nx);
y = linspace(0,2,ny);
z = linspace(0,3,nz);
[X Y Z] = meshgrid(x, y, z);

若采用上述命令来生成[X Y Z], 则

1
2
3

> size(X)
ans
    [ny, nx, nz]

可以发现其第三维的维度没变，而前两维的维度互换。而X的维度要与实际数据的维度相对应，因此，在实际操作中，若采用[X Y Z] = meshgrid(x, y, z);的方式来生成网格数据，那么实际数据的维度应为[ny nx nz].

绘图

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

x = (0:nx-1)*dx;
y = (0:ny-1)*dy;
z = (0:nz-1)*dz;

[X, Y, Z] = meshgrid(x,y,z);

figure;
slice(X,Y,Z,vel,0,0,8);  % vel 为绘图数据，其维度为[ny nx nz];
colormap(jet);
shading flat;
xlabel('x (km)');
ylabel('y (km)');
zlabel('z (km)');
set(gca,'ZDir','reverse');  % Z轴反转，常用于地学数据
set(gca,'YDir','reverse');

raw

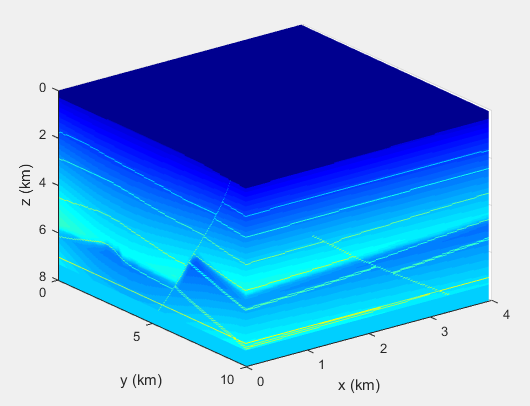
完善细节

图3的主要缺陷是x轴与y轴的label位置未与坐标轴平行，调整的方式为，可将label进行一定程度地旋转，使其与坐标轴平行。

1
2
3
4

x1 = xlabel('x (km)');
y1 = ylabel('y (km)');
set(x1,'Rotation',15);
set(y1,'Rotation',-20);

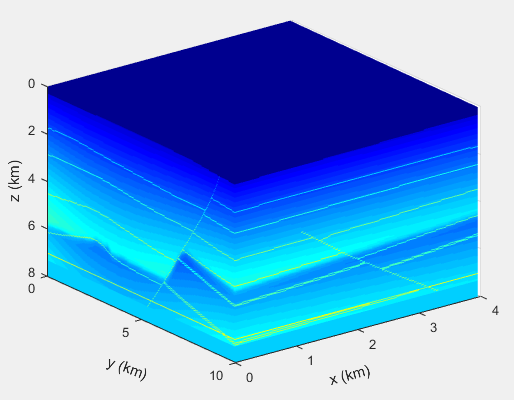
旋转之后的效果见图4

rotate

Reference:

http://blog.sina.com.cn/s/blog_618af1950100eyjn.html

http://muchong.com/html/201206/4636839.html